カルマンフィルタと3次元有限要素法とを組み合わせた逆解析手法は、安定した収束性を得ることができるだけではなく、様々な問題に適用が可能です。ここでは、変形問題を例にとって、変形が生じた場所とその大きさを推定した例を紹介します。

逆解析例：体積ひずみが変化した場所を推定

本手法を用い、地盤内部に何らかの原因で体積ひずみの変化が発生した場合の、発生した場所と体積ひずみの大きさを逆解析により推定してみます。地盤に生ずる体積ひずみ変化としては、間隙水の排出に伴う圧密や二次圧密、熱膨張や収縮、凍結膨張などが考えられます。このような変化が生じた場所が特定できれば、対策工の選定などに貢献します。
このような体積ひずみの発生を応力‐ひずみ関係で示すと、次のようになります。

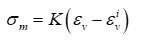
ここに、σmは平均応力、Kは体積弾性定数、ε_vは体積ひずみ、ε_vⁱは何らかの原因で発生した体積ひずみです。
これをもとにをε_vⁱ状態変数とした状態空間モデルを作成し、変位の推定値と観測行列を求めます。その上で、カルマンフィルタによりε_vⁱを推定します。

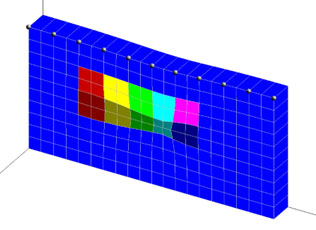
図1に示すモデルを用いて、逆解析の的確さを調べてみます。青色以外の色の付いた10個の領域の内の一つに収縮の体積ひずみを発生させ、モデルに変形を生じさせます。地表面に配置した観測点におけるこのときの鉛直変位を観測値とし、逆解析により体積ひずみが発生した場所とその大きさを推定してみます。ただし、体積ひずみの変化は10個の領域のどれでも生ずる可能性があるものとします。図1では、下の段の右から2番目の領域に収縮の体積ひずみを発生させ、観測値を設定しました。

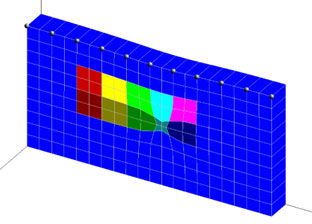
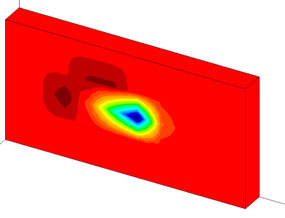
図2が逆解析の結果得られた変形図です。下の段の右から2番目の領域を中心に、収縮の変形が発生していることが推定されています。体積ひずみのコンターを描くと右図下のようになります（青色は収縮）。与えた収縮の体積ひずみ0.1％に対して0.07％程度の収縮ひずみが推定されています。この例では、収縮変形が発生した場所と大きさが、的確に推定されています。