Feel＆Think

第１回でも述べましたが、トンネル掘削や地すべりの解析では、地下水流れと変形の相互作用を考慮できる連成解析が有効です。ただし、地下水流れの解析を適切に行うためには、河川や山の稜線などの分水界を境界とする必要があるため、トンネル径や地すべり範囲に比べてはるかに広い領域が対象となります。このため、解析に用いるメッシュの節点数が大きくなることで、計算時間が長くなってしまう課題があります。
また、連成解析では地下水流れと変形の式を連立させて解くため、自由度が大きく、大規模なモデルでは多くのメモリが必要となります。
この課題を解決するために、地下水流れと変形を別々に解いて近似解を得る方法を検討しました。地下水流れと変形を別々に解くことができれば、例えば、地下水流れを解いておき、必要な時間だけ変形を求めるといったように、計算に要する時間を大幅に短縮することができます。
まず、解くべき方程式を再掲します。

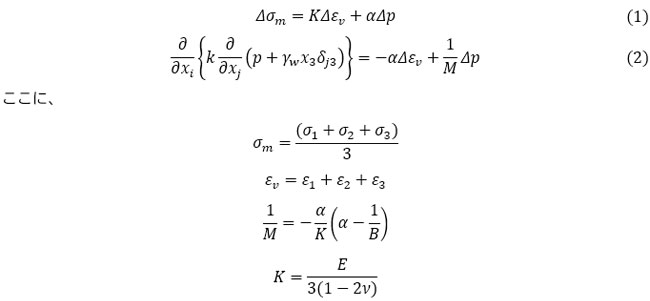
であり、pは間隙水圧、k は透水係数で等方性とします。また、Δは時間増分∂/∂t を表すこととします。
地下水流れと変形を別々に解くためのポイントは、地下水流れの式(2)のε_v を間隙水圧p の関数にすることと、変形の式(1)の間隙水圧p を既知量とすることです。
最初に、地下水流れの式のε_v を間隙水圧p の関数にしてみます。ただし、わかりやすくするために、ｐは過剰間隙水圧（静水圧状態からのずれ量）とします。

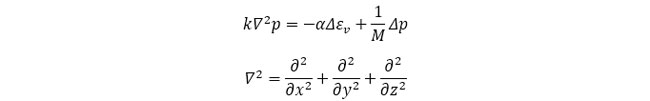
単位時間内に単位体積中を出入りした地下水の体積の差であるΔζ は、次のように記述できます。

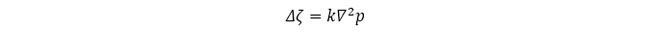
単位体積の要素からΔζ の地下水量の排出があった場合を考えます。

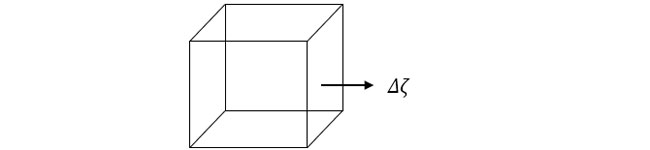
この水の出入りによって、間隙水圧がどう変化するかは、境界条件によります。
仮に、この要素の変形が拘束されている場合は、Δε_v=0 であることから、

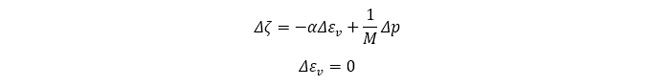
間隙水圧p の変化は次式となります。

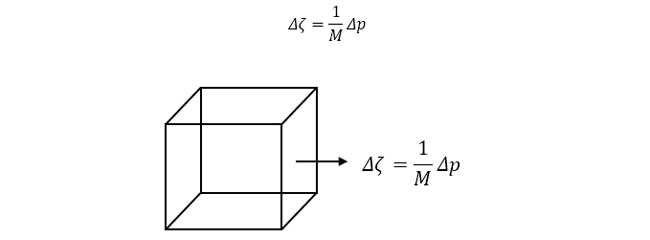
そうではなく自由に変形できる場合は、平均応力σ_m の変化がないことを考慮して、

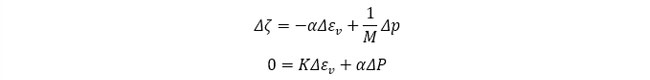
間隙水圧の変化として次式が得られます。

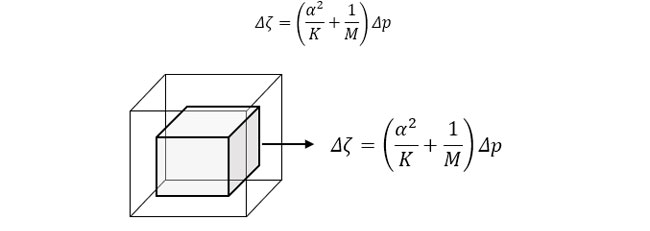
実際の現象は、これら二つの両極端の現象の間にあることから、両式を足し合わせて平均を取ることにします。

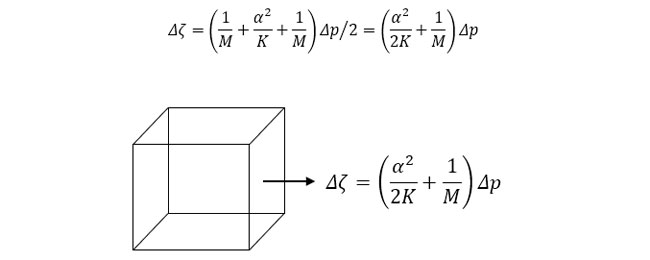
これで、地下水流れの式を間隙水圧p のみの関数とすることができました。いわゆる浸透流解析の式です。

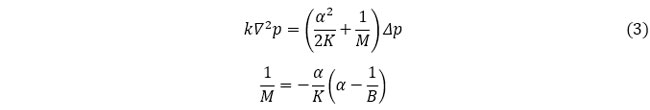
一方、変形の式は、上式の解として得られる間隙水圧p(t) を既知量として解きます。

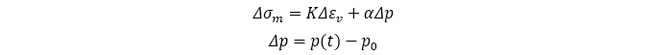
したがって、変形の式は時間に関係なく解くことができます。
以降に示すとおり、上式右辺の係数を用いることで、連成解析と擬似連成解析の解はよい近似度を示します。

■圧密問題による検証

この疑似連成解析がどの程度の近似を得られるかを、第2回で用いた圧密問題で試してみましょう。

用いた解析条件を下表に一覧します。

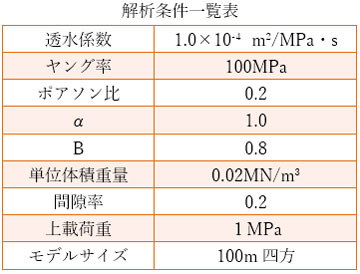
以下の3ケースで解を比較しました。

ケース3では、計算時間の大幅な短縮が期待できます。
解析結果を以下に示します。この例では、完全連成解析と疑似連成解析で解は一致します。

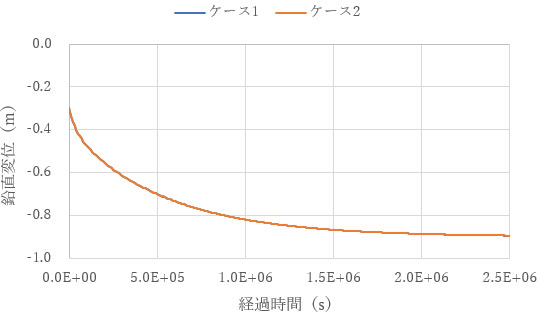
間隙水圧の変化も一致しています。

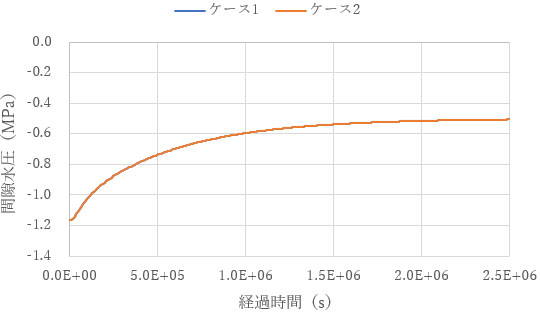
浸透流解析の結果を任意の時間で変形解析に渡した場合（ケース３）でも、その時間の変形は一致します。この場合はΔt 毎に変形の計算をする必要がなく、計算時間が大幅に短縮されます。

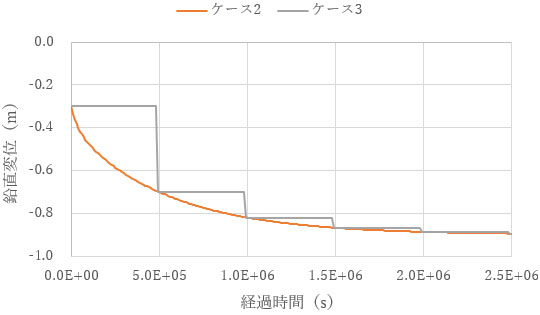
なぜこのような一致が見られるのでしょうか。第2回で示した1次元圧密方程式は、次のようなものでした。

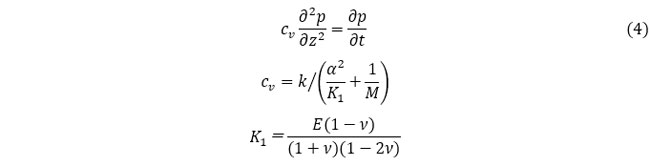
これまで使ってきた記号で記述すると、次のようになります。

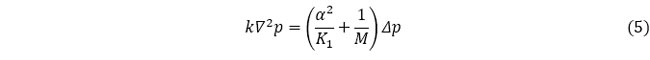
ここで、K₁ に注目すると、

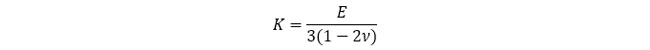
であることから、

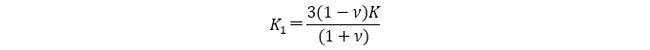
と書くことができます。
今回の解析では、ν＝0.2としていることから、

となり、圧密方程式は式(3)に一致します。

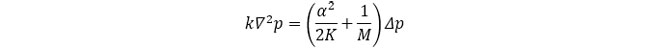
このことは、K₁ に 現れる が境界条件の影響を表しており、ν＝0.2の場合に、たまたま圧密方程式が近似式(3)と一致することを示しています。圧密方程式は完全連成解析の支配方程式そのものであることから、ν＝0.2の場合に完全連成解析の解と擬似連成解析の解とが一致することがわかります。
では、ν が0.2以外の場合はどの程度の近似度が見込まれるのでしょうか。
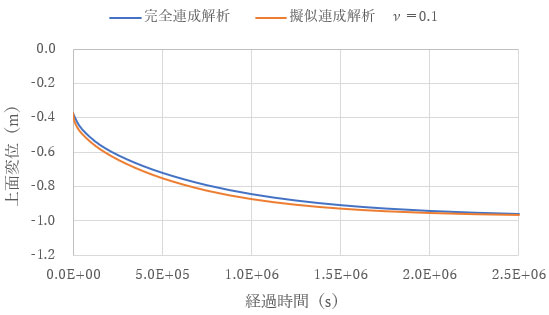
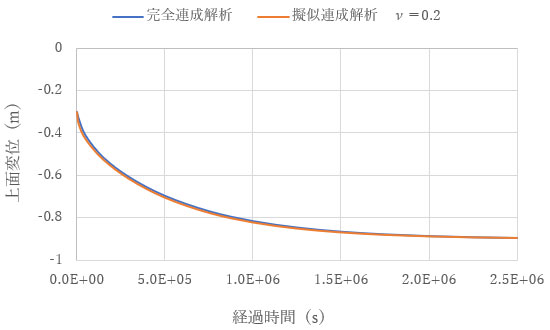
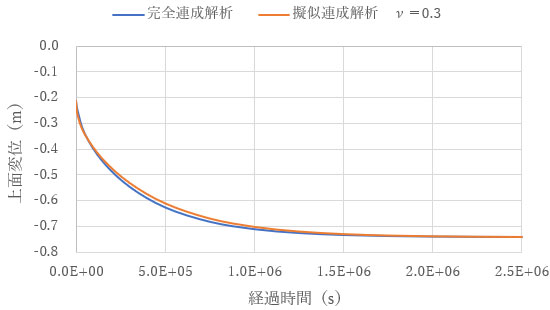
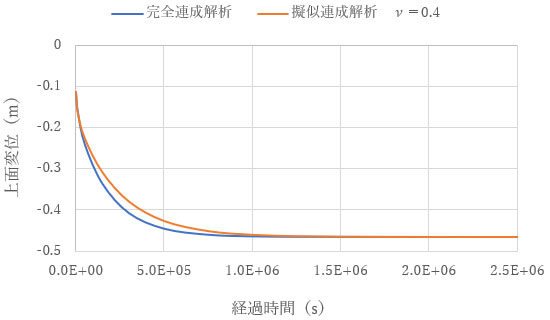
下図は、ν を0.1から0.4に変化させて描いた圧密沈下曲線です。ν が0.1から0.3では、完全連成解析と擬似連成解析の差は全変位に対して5％程度で、0.4の場合は10％程度であることがわかります。土や岩盤の排水条件での ν は0.2から0.3であることから、提案した近似式(3)を用いることで、完全連成解析に対して擬似連成解析が良い近似を与えることが示されました。

次回は、トンネルからの湧水を例にして完全連成解析と擬似連成解析を比較します。