Feel＆Think

前回の「生成AI」では、現在提供されている製品やサービスについて、文章生成AI、画像生成AI、動画生成AI、3Dモデル生成AIに分けて、紹介しました。また、生成AIを活用するうえで、経営層の重要性に焦点をあてて解説しました。

今回は、以前紹介した強化学習についてその基礎となる「マルコフ決定過程」、「ベルマン方程式」、「動的計画法」、「モンテカルロ法」について説明していきます。

マルコフ決定過程

■マルコフ決定過程って何？

マルコフ決定過程（Markov decision process, MDP）は、選択と結果の関係を扱うための数学的なフレームワークです。たとえば、迷路の中でどちらの道を進むかを決めるときに使います。MDPは、現在の状態（状態）、次に取る行動（行動）、その結果次に移る場所（遷移）、そして得られる報酬（報酬）をまとめたものです。

■どんなときに使うの？

MDPは、ロボットの動作計画、ゲームの戦略決定、経済学における意思決定など、多くの場面で使われます。

■MDPの構成要素

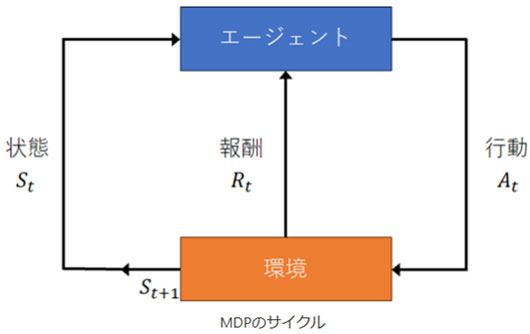
状態（State）
状態とは、システムが現在どのような状況にあるかを示します。たとえば、迷路の中での現在の位置が状態です。
　例: 迷路の特定の位置、チェスの現在の盤面

行動（Action）
行動とは、現在の状態で取ることができる選択肢です。迷路なら右に行くか左に行くかを選ぶことです。
　例: 右に進む、左に進む、攻撃する、防御する

遷移（Transition）
遷移とは、ある状態から次の状態への変化です。これは特定の行動を取った結果として起こります。迷路で右に進むと、次の場所に移動することが遷移です。
　例: 「A地点から右に行くとB地点に移動する」

報酬（Reward）
報酬とは、特定の行動を取った結果として得られる価値やポイントです。迷路で正しい道を選んだら宝物がもらえるようなものです。
　例: 宝物、ポイント、経験値

■MDPの例で学ぶ

迷路ゲーム
迷路の中でどちらに進むかを決めるゲームを考えてみましょう。これがマルコフ決定過程の簡単な例です。

1. 状態：迷路の現在の位置
2. 行動：右に行く、左に行く、上に行く、下に行く
3. 遷移：行動をとった結果、どこに移動するか
4. 報酬：正しい道を選んだらポイントがもらえる

チェス
チェスの試合でもMDPを適用できます。

1. 状態：現在の盤面の配置
2. 行動：駒を動かす
3. 遷移：駒を動かした結果の新しい盤面配置
4. 報酬：駒を取った場合のポイント、最終的な勝利

■最適な行動を見つける方法

ベストな行動を選ぶ
MDPの目的は、将来の報酬を最大化するための最適な行動を見つけることです。これは「最適化」と呼ばれ、数学的に計算することができます。最適な行動を選ぶために、現在の状況と未来の見通しを考慮します。

強化学習
強化学習は、エージェントが環境と相互作用しながら最適な行動を学ぶ方法です。例えば、ゲームの中でいろいろな技を試して、どの技が一番効果的かを学ぶことです。

• Q学習（Q-Learning）: 各状態での行動の価値を学び、最適な行動を選ぶ方法。行動価値関数Qを更新しながら最適解を求めます。
• SARSA: 実際の行動方針に基づいて価値を更新する方法。行動を選びながら次の状態と報酬を学習します。
• エピソードと学習：強化学習では、エピソード（試行）を通じて学習します。例えば、ゲームのプレイを何度も繰り返し、経験を積んで学習します。これにより、どの行動が最も効果的かを見つけることができます。

ベルマン方程式

■ベルマン方程式って何？

ベルマン方程式は、マルコフ決定過程（MDP）において最適な行動方針を見つけるための基本的な方程式です。リチャード・ベルマンという数学者によって提唱されました。簡単に言うと、未来の報酬を考慮しながら現在の最適な行動を決定する方法です。

■どんなときに使うの？

ベルマン方程式は、強化学習や最適化問題で広く使われます。例えば、迷路を解くロボットや、ゲームの戦略を決めるときに役立ちます。

■ベルマン方程式の基本概念

状態価値関数（State Value Function）
状態価値関数V ^π(s)は、ある状態 s にいるときに期待される累積報酬のことです。簡単に言うと、その状態がどれだけ「良い」かを示します。
　例: 迷路の中でゴールに近い位置ほど価値が高い

行動価値関数（Action Value Function）
行動価値関数 Q ^π(s,a)は、状態 s で行動 a を取ったときに期待される累積報酬のことです。これは、特定の行動を選んだときに得られる価値を示します。
　例: 迷路の特定の位置で右に進む価値

割引率（Discount Factor）
割引率 γ は、未来の報酬の価値を現在と比べてどれだけ低く見積もるかを示します。これは、未来の報酬が現在の報酬に比べてどれだけ重要かを決めるパラメータです。
　例：γ = 0.9 なら、未来の報酬は90%の価値で評価されます

■ベルマン方程式の導出

状態価値関数のベルマン方程式
状態価値関数V ^π (s)のベルマン方程式は次のように表されます：

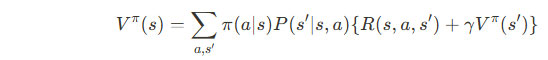
ここで、

• π（a｜s）：状態 s において行動 a を選択する確率
• P（s’｜s,a）：状態 s において行動 a を取ったときに次の状態 s’ になる確率
• R（s,a）：状態 s で行動 a を取ったときに得られる報酬

行動価値関数のベルマン方程式
状態価値関数Q ^π (s,a)のベルマン方程式は次のように表されます：

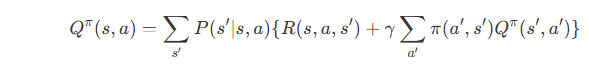
ここで、

• a’：次の状態での最適な行動

■ベルマン方程式の応用

迷路ゲーム
迷路の中で最適な道を見つけるために、ベルマン方程式を使って各位置の価値を計算します。例えば、ゴールに近い位置ほど価値が高くなるように計算します。

経済学の意思決定
ベルマン方程式は、経済学においても企業の投資戦略や消費者の購買行動をモデル化するために使われます。将来の利益を最大化するための現在の最適な行動を決定します。

■ベルマン方程式の解法

動的計画法（Dynamic Programming）
動的計画法を使って、ベルマン方程式を効率的に解くことができます。これは、現在の問題を小さな部分問題に分割し、再帰的に解く方法です。
　例: フィボナッチ数列の計算も動的計画法で効率的に解けます

値反復法（Value Iteration）
値反復法は、ベルマン方程式を繰り返し適用して状態価値関数を更新する方法です。これを何度も繰り返すことで、最終的に最適な価値関数を見つけます。
　例: 迷路の各位置の価値を何度も更新して最適な道を見つける

方策反復法（Policy Iteration）
方策反復法は、まず初期の行動方針を設定し、その方針に基づいて価値関数を計算し、次に方針を改善する方法です。これを繰り返すことで、最適な方針を見つけます。
　例: 最初はランダムに進み、徐々に最適な道を見つける

動的計画法

■動的計画法って何？

動的計画法（Dynamic Programming, DP）は、複雑な問題を小さな部分問題に分割し、それらを解くことで全体の問題を効率的に解決する方法です。主に最適化問題や組み合わせ問題で使われます。

■どんなときに使うの？

動的計画法は、経路探索、ナップサック問題、フィボナッチ数列の計算など、さまざまな場面で使われます。例えば、迷路の中で最短経路を見つけるときなどです。

■動的計画法の基本概念

メモ化とタブラリゼーション
動的計画法には2つの主要なアプローチがあります：メモ化とタブラリゼーション。

• メモ化（Memoization）: 再帰的な関数呼び出しで、すでに計算した結果を保存し、再利用する方法です。これにより、同じ計算を何度も繰り返すことを防ぎます。
• タブラリゼーション（Tabulation）: 問題を小さな部分問題に分割し、それらをテーブルに格納し、順に解いていく方法です。これは、ボトムアップアプローチとも呼ばれます。

最適部分構造と重複部分問題
動的計画法が適用できる問題は、最適部分構造と重複部分問題の2つの特性を持っています。

• 最適部分構造（Optimal Substructure）: 問題の最適解が、その部分問題の最適解から構成される特性です。
• 重複部分問題（Overlapping Sub-problems）: 問題を解く際に同じ部分問題が何度も計算される特性です。

■動的計画法の具体例

－フィボナッチ数列

フィボナッチ数列は、次のように定義される数列です：

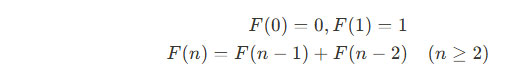
再帰的に計算すると多くの重複計算が発生しますが、動的計画法を使うと効率的に計算できます。

メモ化を使った解法

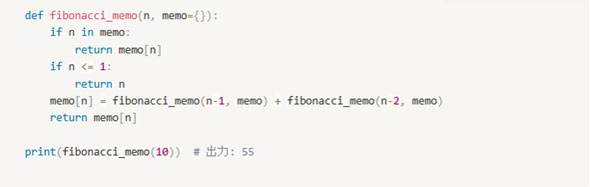
タブラリゼーションを使った解法

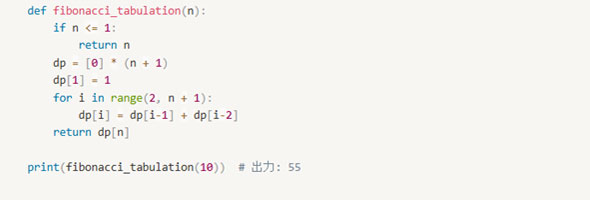
－ナップサック問題

ナップサック問題では、限られた容量のバッグに最大の価値を詰め込む方法を見つけます。

問題設定
・アイテムの価値と重量：（v₁，w₁），（v₂，w₂），….. ，（v_n，w_n）
・バッグの重量：W

解法
動的計画法を使って価値の最大化を図ります。

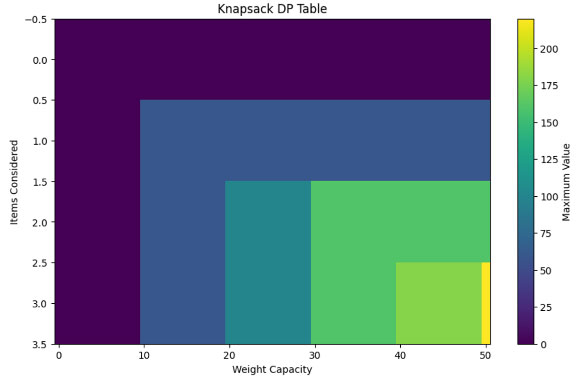
■動的計画法の応用

経路探索
迷路の中でスタートからゴールまでの最短経路を見つけるために動的計画法を使います。例えば、各位置までの最短距離をテーブルに記録し、順次更新していく方法です。

文字列操作
文字列の編集距離（レーベンシュタイン距離）を計算するためにも動的計画法を使います。これは、ある文字列を別の文字列に変換するための最小操作回数を求める問題です。

経済学や金融
経済学や金融において、投資戦略やポートフォリオの最適化問題を解くためにも動的計画法が使われます。これにより、リスクとリターンのバランスを取った最適な投資計画を立てることができます。

■動的計画法の実践

アルゴリズムの設計
動的計画法を実践する際には、以下のステップを踏みます：

1. 問題の部分問題を定義する
2. 再帰的な関係を見つける
3. メモ化またはタブラリゼーションを使って部分問題を解く
4. 最終的な問題を解決する

効率的な実装
効率的な実装のためには、メモリ使用量と計算時間を考慮することが重要です。例えば、不要な計算を避けるために、必要な部分だけを計算するようにします。

モンテカルロ法

■モンテカルロ法って何？

モンテカルロ法は、複雑な問題を解くためにランダムなサンプリングを使う方法です。名前は、モンテカルロというカジノがあるモナコ公国に由来します。ギャンブルのようにランダムな試行を使って問題を解決するという意味で名付けられました。

■どんなときに使うの？

モンテカルロ法は、物理学、金融工学、統計学など、さまざまな分野で使われます。たとえば、円周率（π）の近似値を求めることや、株価の予測などに役立ちます。

■モンテカルロ法の基本概念

ランダムサンプリング
モンテカルロ法の基本は、ランダムサンプリングです。これは、ランダムな値を使って問題を解く方法です。多くの試行を繰り返すことで、正確な結果に近づけます。
　例: ダーツを投げて、的中率から円周率を求める

期待値と確率
モンテカルロ法では、期待値と確率を使って結果を導きます。期待値とは、ある試行の平均的な結果を示します。確率は、ある出来事が起こる可能性を示します。
　例: コインを100回投げて、表が出る確率を求める

■モンテカルロ法の具体例

－円周率（π）の近似

モンテカルロ法を使って円周率を近似する方法を見てみましょう。

問題設定

1. 単位正方形の中にランダムに点を打つ
2. その点が単位円（半径1の円）の中に入るかどうかを判定
3. 点の総数に対する円の中に入った点の割合からπを近似

解法

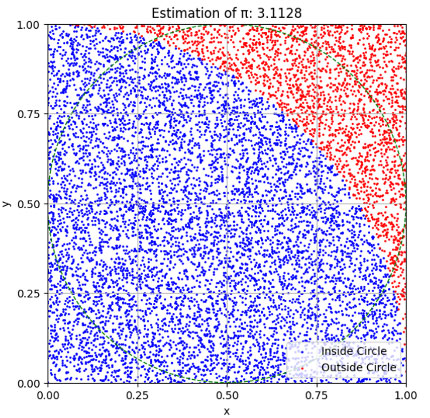
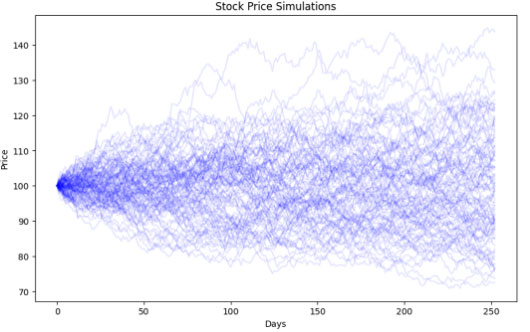
－株価の予測

モンテカルロ法は、株価の予測にも使われます。ランダムな変動を仮定して、多くのシナリオをシミュレーションし、将来の株価の分布を求めます。

問題設定

1. 現在の株価と過去の変動を基に、ランダムな変動を仮定
2. 多くのシナリオをシミュレーション
3. シミュレーション結果の平均や分布を分析

解法

■モンテカルロ法の応用

物理学のシミュレーション
物理学では、モンテカルロ法を使って粒子の動きや熱力学的性質をシミュレーションします。例えば、原子や分子の振る舞いをモデル化するために使われます。

統計学の推定
統計学では、モンテカルロ法を使ってパラメータの推定や仮説検定を行います。大規模なデータセットの分析や確率分布の近似に役立ちます。

ゲーム理論
ゲーム理論では、モンテカルロ法を使って最適な戦略を見つけます。例えば、ポーカーやチェスなどのゲームで最適な手を見つけるために使われます。

■モンテカルロ法の実践

アルゴリズムの設計
モンテカルロ法を実践する際には、以下のステップを踏みます：

1. 問題の定義
2. ランダムなサンプリング方法の決定
3. サンプリングを繰り返す
4. 結果の集計と分析

効率的な実装
効率的な実装のためには、計算時間とメモリ使用量を考慮することが重要です。多くのサンプリングを行う場合には、並列計算を使うことも効果的です。

まとめ

マルコフ決定過程（MDP）は、意思決定を数学的にモデル化するための強力なツールです。状態、行動、遷移、報酬という4つの要素を使って、複雑な問題を解決することができます。MDPを理解することで、ゲームの戦略やロボットの動作計画など、さまざまな実世界の問題に応用することが可能です。

ベルマン方程式は、マルコフ決定過程における最適な行動方針を見つけるための強力なツールです。状態価値関数や行動価値関数を使って、将来の報酬を考慮しながら現在の最適な行動を決定します。これにより、ゲームの戦略やロボットの動作計画、経済学の意思決定など、さまざまな実世界の問題を解決することができます。

動的計画法（Dynamic Programming）は、複雑な問題を効率的に解決するための強力なツールです。最適部分構造と重複部分問題の特性を利用して、経路探索やナップサック問題など、さまざまな問題を解決することができます。動的計画法をマスターすることで、複雑なアルゴリズムを効率的に設計し、実世界の問題に応用する力を身につけることができます。

モンテカルロ法は、ランダムなサンプリングを使って複雑な問題を解決するための強力なツールです。物理学、金融工学、統計学など、さまざまな分野で応用されています。モンテカルロ法を理解し、実践することで、複雑なシミュレーションや予測を効率的に行う力を身につけることができます。

今回は、強化学習についてその基礎となる「マルコフ決定過程」、「ベルマン方程式」、「動的計画法」、「モンテカルロ法」について説明しました。次回は、引き続き強化学習おける基礎となる「TD法」、「ニューラルネットワークとQ学習」、「DQN」、「方策勾配法」について詳しく紹介していきます。

---

参考資料
１）ゼロから作るDeep Learnig(4)－強化学習編（書籍・オライリージャパン・2022/4/6発行）
２）強化学習 (機械学習プロフェッショナルシリーズ) （書籍・講談社・2019/発行）